What are algorithms and how are they used in control engineering?

These algorithms (Google, Facebook, Tik Tok, etc.), behave like a virtual librarian, selecting the best things for you to see, or read. This clever librarian knows what books you read in the past, they know which book you are choosing now, and they have some information about the new things that will interest you in the future. With this knowledge they can recommend the books, magazines, and videos that will probably interest you.
An algorithm is, in general, a set of step-by-step instructions or rules to solve a problem or perform a task. According to this simple definition, a recipe in a cookbook is an algorithm, and so is a business process, a software program, or a flowchart.
Mathematicians and engineers generally think of an algorithm as a set of clearly defined, logical steps in a process to calculate something. Algorithms are used in many fields, such as computer science, mathematics, and daily life, to make processes and tasks more efficient.
Simple examples of algorithms
A very simple algorithm is to calculate S, the sum of two numbers, X and Y.
Start process:
Add X and Y to calculate S (i.e. X+Y = S)
Stop process.
A more sophisticated example is an algorithm used to find out if a given number (N) is a prime:
Start process:
Divide the number (N) by 2, then
Divide the number (N) by 3, then
… continue the process, until finally…
Divide the number (N) by N-1
If none of these calculations results in a whole number, then N is prime.
Stop process.
(Note: in practise, only calculate up to √N)
Another type of algorithm is a logical statement, such as “if something is true, then do task A”; and “if that thing is false, then do task B”. For example: “if you are guilty, you will go to prison”; and “if you are innocent, you will be free”.
Start process:
You are guilty? Answer “Yes”; then you go to prison.
You are guilty? Answer “No”; then you are free.
Stop process.
The use of algorithms in control engineering

Let’s look at the use of algorithms in control engineering, starting with “on/off” control.
As an example, room temperature can be controlled by a thermostat using a simple on/off control algorithm:
- If room is too warm, then turn the heating off.
- If room is too cold, then turn the heating on.
This type of control is like the “go to prison” algorithm: If A is true, then do X; if B is true, then do Y, as described above. It is called an “on/off” control algorithm because the heating (in this case) is either fully on or fully off until the desired state (temperature) is reached.
Proportional control algorithm
Another simple algorithm is called Proportional control which is used, e.g., in automatic speed control of a vehicle by opening and closing the throttle:
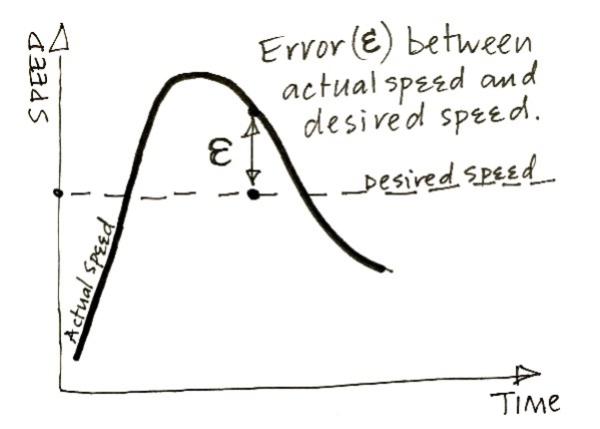
- If actual speed is too low, then partly open throttle; and
- If actual speed is too high, then partly close throttle.
The difference between the desired speed and the actual speed is called the error (ε), as shown on the right. This error (ε) varies as the actual speed changes with time. It is, of course, zero when the actual speed is equal to the desired speed.
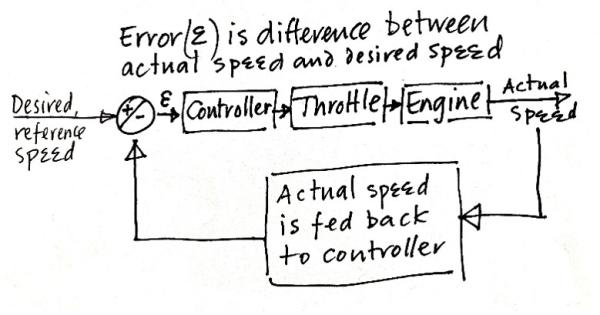
The actual speed at any time is fed back to the speed controller (as shown on the left), which then calculates the difference (error ε) between the actual speed and the desired speed, and then opens the throttle in “proportion” to the size of this error (ε): if the error is big, then open the throttle a lot; and if the error is small, then open the throttle a little. (as shown on the left), which then calculates the difference (error ε) between the actual speed and the desired speed, and then opens the throttle in “proportion” to the size of this error (ε): if the error is big, then open the throttle a lot; and if the error is small, then open the throttle a little.
Proportional control algorithms, that increase or decrease the input to a system (in this case the vehicle) in proportion to the error, work well in many cases. However, there can be challenges, requiring a more sophisticated control algorithm. For example, with a proportional control algorithm, there can be big swings, or overshoots, before converging on the desired speed. There can also be a long-term error, or offset, between the desired and the actual speed, which never goes away.
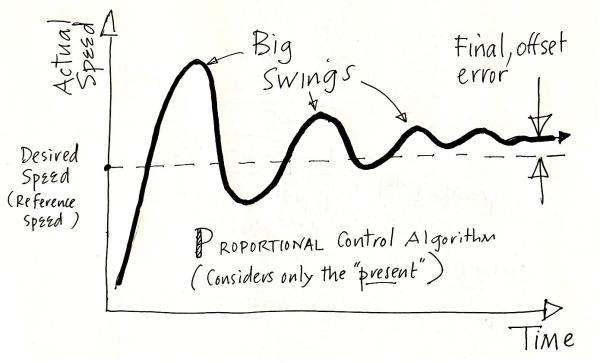
Control with PID algorithm
In some control systems these problems are significant, and a more sophisticated algorithm, called a PID algorithm (Proportional, Integral, Differential), is needed. Without going into the mathematics, the PID algorithm behaves like the virtual librarian, in that it considers the present, the past, and the future state of a system.
The “Proportional” part of the algorithm represents the present: i.e. the controller opens the throttle in proportion to the present error: i.e. in proportion to the present difference between actual speed and desired speed.
The “Integral” part of the algorithm responds according to the past: it adds up the errors from the past and makes additional, small adjustments in the throttle opening so that the output converges precisely on the desired speed, with no final, offset error.
The “Differential” part of the algorithm represents the future: it looks to see if the error is changing so fast that the system will overshoot the desired output value, and it then makes corresponding, additional adjustments to the throttle opening.
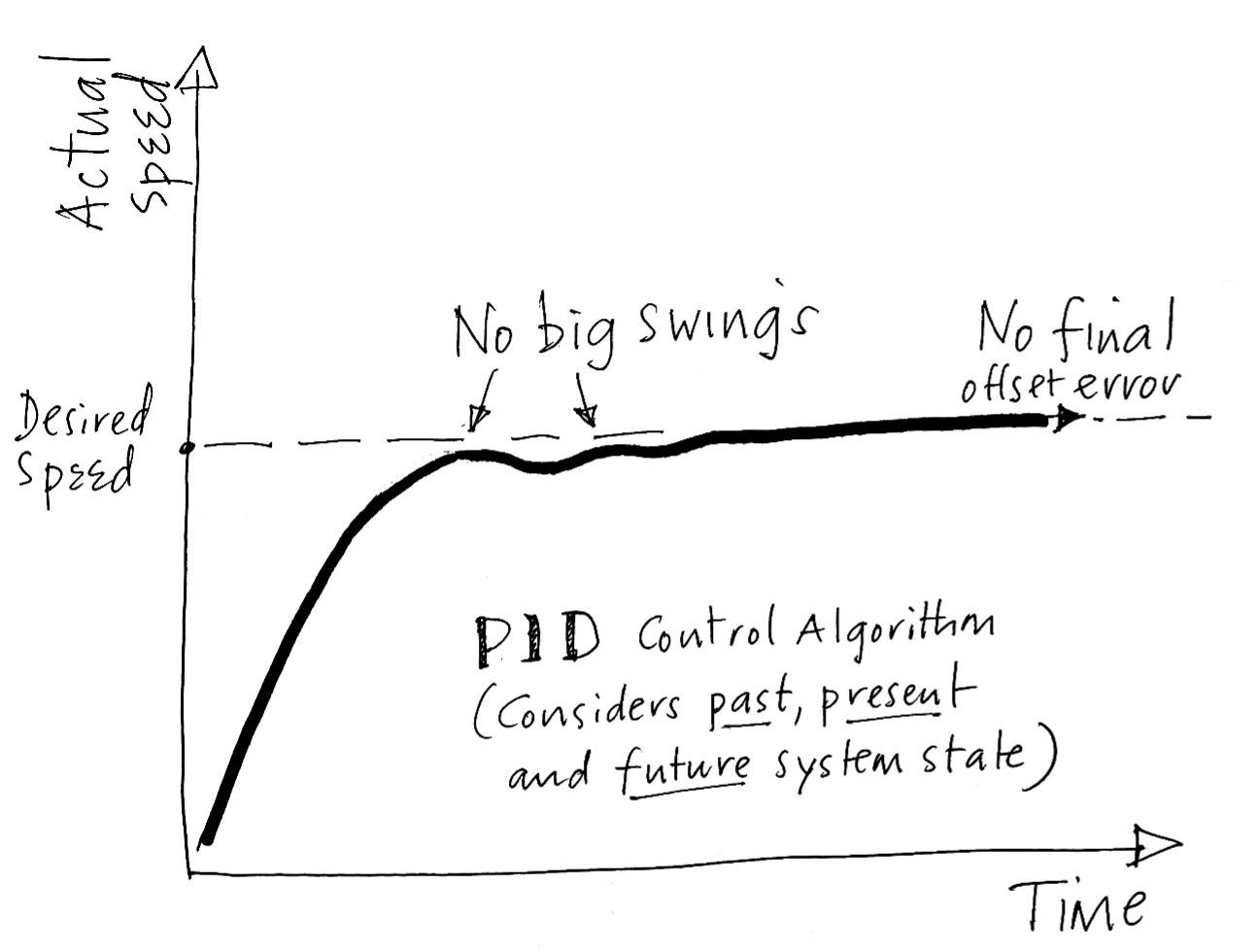
Here (in the figure, below), we see the result of speed control with a PID algorithm. There are no big swings or overshoots. The speed converges on the desired speed, accurately and smoothly, and there is no final offset error.
There are other, much more sophisticated algorithms that apply in complex situations, such as controlling a robot arm in a factory, where there are multiple outputs to be controlled; or systems for which there is no one correct output, rather like the social media algorithms, where you just aim for a good solution.
By Jonathan Copley



