Comprendre la forme de la stabilité

Chaque matin, pour me rendre à l'EPFL, je canalise le Mathieu van der Poel qui sommeille en moi et je pédale sur les collines de Lausanne. Malgré ma maladresse et avant d'avoir bu un nombre suffisant de cafés, je ne tombe pas, typiquement. Des cailloux sur la route, un coup de vent, ou un virage rapide pour éviter de croiser des vaches (nous sommes dans les Alpes, après tout) sont autant de perturbations qui peuvent être facilement gérées, apparemment sans aucun effort. Cela n'a pas grand-chose à voir avec mes compétences en matière de maniement du vélo, et tout à voir avec la notion mathématique de stabilité.1
En termes simples, un système - par exemple, moi sur le vélo - est dit stable* lorsqu'il revient toujours à son état nominal en cas de petites perturbations. C'est exactement ce que nous vivons. Une rafale de vent me bouscule un peu, mais je me rétablis toujours et je reviens à mon état nominal, qui est d'aller tout droit. Des phénomènes similaires se produisent en avion (pensez aux turbulences), en bateau (avec des perturbations presque constantes sous forme de vent et de vagues) ou en prenant le métro de Lausanne Flon à Lausanne Gare, qui est un test sérieux pour notre système d'équilibre interne.
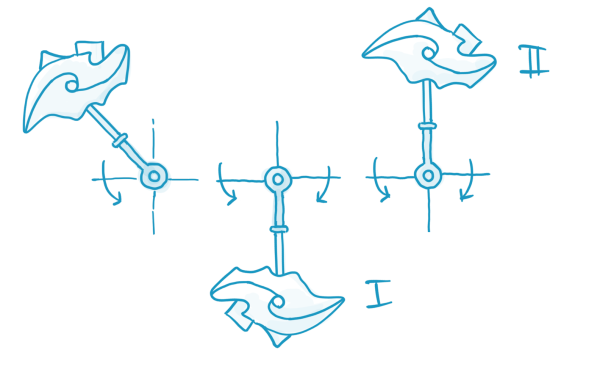
Alors, comment se fait-il que quelque chose ne soit pas stable ? C'est le cas lorsqu'il n'est pas possible de se remettre d'une perturbation arbitrairement petite. Le pendule est un exemple éloquent (qui se trouve être la pierre angulaire d'un grand nombre d'analyses dans notre domaine). Un pendule est essentiellement une tige, montée de manière à pouvoir tourner librement, avec une extrémité suffisamment lourde. Dans l'état (I) comme dans l'état (II), le pendule est au repos, mais notez que seul l'état (I) est stable : nous pouvons pousser un peu le pendule et il reviendra à l'état de repos. Si nous poussons le pendule dans l'état (II), même très légèrement, il ne reviendra pas à l'état (II) ; l'état (II) est instable.
Vous pouvez le tester vous-même : essayez de faire tenir un stylo en équilibre sur votre main et ne bougez pas. Que se passe-t-il si vous poussez un peu le stylo ? Bien sûr, la difficulté d'essayer de faire tenir le stylo en équilibre sur votre main en dit déjà long. Si vous essayez avec différents objets, vous remarquerez que la "vitesse de chute" change ; un grand bâton avec un sommet lourd se comporte très différemment d'un stylo à bille. On peut se poser la question suivante : si cette chute était extrêmement lente, si lente que nous, les humains, ne pourrions pas l'observer avec nos yeux, pourrions-nous même faire des commentaires sur sa stabilité ?
Tous ces exemples sont quelque peu tangibles, mais la notion de stabilité s'étend bien au-delà du domaine mécanique. En particulier dans ces contextes moins tangibles, nous aimerions comprendre la stabilité par des méthodes plus complètes que la simple observation. Pensez au système solaire : nous ne savons pas d'où nous venons, mais pouvons-nous au moins dire où nous allons ? Dans dix milliards d'années, serons-nous encore en train de tourner autour du soleil ?
Cet exemple est fascinant pour plusieurs raisons. Tout d'abord, pour parler de stabilité, il faut avoir une certaine compréhension du comportement du système. Qu'est-ce qui est normal, qu'est-ce qui est souhaité ? Le désir d'améliorer notre compréhension a inspiré des branches entières des mathématiques et de la physique. Deuxièmement, l'énorme échelle en jeu complique considérablement les expériences physiques et, dans une certaine mesure, les mesures ; idéalement, nous aimerions donc nous contenter d'analyser les modèles mathématiques de la physique pour tirer nos conclusions. Tenter de répondre à ces questions est un effort constant depuis l'époque de Newton.2
Que se passe-t-il si de petits changements deviennent de grands changements ?
Il est évidemment important de comprendre la stabilité du système solaire, mais nous sommes confrontés à des problèmes plus urgents : prenons l'exemple du changement climatique. Le climat, en tant que système, est extrêmement complexe et fait l'objet d'études approfondies. Prenons un exemple particulier, celui du système glace-albédo. Dans des conditions idéales, la quantité de lumière solaire absorbée par nos océans et nos terres est en équilibre avec la quantité de lumière solaire réfléchie par la glace de nos calottes polaires.
Mieux encore, dans des conditions idéales, nous pouvons espérer que ce système est stable, c'est-à-dire que de petites variations dans la quantité d'eau, de terre et de glace ne modifient pas de manière significative la température sur terre. Cependant, si le système glace-albédo est suffisamment perturbé, par exemple par l'introduction d'un excès de gaz à effet de serre, la fonte des calottes polaires rompt cet équilibre. En conséquence, la lumière du soleil est moins réfléchie, la terre se réchauffe, la glace fond davantage et ainsi de suite, formant une boucle de rétroaction destructrice.3
Cela montre comment un changement dans le système peut modifier la stabilité, par exemple en passant de stable à instable. Il est essentiel de comprendre ce phénomène, en particulier dans le contexte du changement climatique. De nombreux autres exemples peuvent être trouvés, une grande partie de la recherche se concentrant sur les sciences de la vie. En médecine, par exemple, vous pouvez avoir un système instable (pensez au cancer) que vous voulez rendre stable (arrêter la croissance de la tumeur et anéantir le cancer). Dans ce cas, nous voulons stabiliser le système. Autrement dit, nous ne voulons pas seulement décrire la dynamique d'un système, nous voulons comprendre ce qui peut être prescrit ; c'est l'étude de la théorie du contrôle.
Les exemples que nous avons vus jusqu'à présent sont tous physiques, mais lorsque vous regardez les nouvelles, tout est "en ligne" et "IA". Cette nouvelle réalité en ligne est-elle stable ? Cette question fait l'objet de recherches actives, mais permettez-moi de vous donner quelques exemples. Par exemple, un service de streaming comme Spotify recommande de la musique en fonction de ce que vous et vos pairs écoutez. En tant qu'utilisateur, vous souhaitez que cela soit stable ; après avoir écouté vos groupes de thrash metal préférés pendant des années, une seule écoute de la bande originale de Barbie ne devrait pas changer radicalement vos listes de lecture (vos voisins pourraient ne pas être d'accord).
Si vous avez lu un précédent article du blog du PRN sur la descente de gradient, vous trouverez un exemple plus technique. Lorsqu'il est appliqué à un problème convexe, le processus est stable ; lorsqu'il est appliqué à un problème non convexe, nous risquons de nous retrouver bloqués. En d'autres termes, dans le langage ci-dessus, nous ne nous "remettons" pas toujours d'une perturbation qui nous éloigne de l'optimiseur. En ce qui concerne les algorithmes, d'autres aspects peuvent compromettre la stabilité : des données imparfaites (par exemple, des images floues utilisées pour la reconnaissance d'objets) ou simplement le fait que les machines numériques travaillent avec une précision finie (nous ne pouvons pas stocker des séquences de nombres infiniment longues sur un ordinateur).
À présent, vous êtes probablement d'accord pour dire que la stabilité est importante, mais qu'il n'est pas facile de l'identifier, et encore moins de l'imposer. En outre, nous espérons que ces exemples vous ont convaincu que, 300 ans après Newton, il est toujours utile d'étudier la stabilité, peut-être aujourd'hui plus que jamais.
Quel est le rapport avec la forme ?
En étudiant la stabilité, nous nous attachons en particulier à comprendre quand la stabilisation est possible. Quelles sont les caractéristiques qui permettent à un système d'atteindre la stabilité - ou qui l'interdisent ?
Bien qu'il ne s'agisse pas de l'exemple le plus passionnant, revenons au pendule. Nous avons dit que l'état (I) (pendu) est stable, mais nous pouvons être plus précis. L'état (I) est stable par rapport à toute perturbation, sauf si nous nous retrouvons d'une manière ou d'une autre dans l'état (II) (être au repos dans la position ascendante). Autrement dit, l'état (I) est un état globalement stable du système pendulaire ;
Pour mieux comprendre, imaginons que le pendule est une bille qui roule sur la crête d'une colline, comme l'illustre la figure 3. Là encore, la bille peut être au repos dans l'état (I) ou dans l'état (II). Mais ; l'état (I) est presque globalement stable, tandis que l'état (II) est à nouveau instable. Pouvons-nous déformer l'arête en douceur de manière à ce que l'état (I) soit globalement stable ? Cela signifierait que, tout au long de la trajectoire de l'arête, il ne devrait y avoir qu'une seule position où la balle pourrait s'immobiliser.

Pour tester cela, prenez un rouleau de papier toilette vide et une paire de ciseaux. Pouvez-vous découper une courbe lisse qui ne présente qu'une "vallée" (comme l'état (I) du pendule) ou qu'un "sommet" (comme l'état (II)) ? Malheureusement, cela ne fonctionne pas : vous ne pouvez pas avoir le sommet sans la vallée, et vice versa. Il est donc impossible, quelle que soit la variation de cette forme, de parvenir à une stabilité globale.
Le nœud du problème est la forme circulaire de notre crête. Tout mouvement s'éloignant du sommet signifie que l'on descend ; mais à un moment donné, en contournant le sommet, on commence à monter (sinon nous serions dans le monde d'Escher)... et cela crée un deuxième point où notre balle imaginaire peut être au repos. La forme du cercle fait obstacle à la stabilité globale.
Cette simple observation est importante car elle permet de tirer des conclusions assez fortes, basées sur peu d'hypothèses. Nous n'avons pas eu besoin de nous préoccuper de la forme bizarre de notre pendule, mais seulement de la forme de sa trajectoire. C'est ce qui m'intéresse. Avec plusieurs collègues et avec le soutien du Fonds national suisse de la recherche scientifique, j'ai étudié la manière dont la "forme" sous-jacente d'un système dicte ce qui est possible, bien au-delà d'un point sur un cercle.
L'une des principales conclusions est que pour les problèmes véritablement non linéaires, la topologie sous-jacente joue un rôle clé - peut-être le rôle clé - dans la compréhension, et potentiellement la réalisation, de la stabilité. Et le monde est non linéaire... "Pour comprendre ce à quoi nous faisons allusion, il serait bon de réfléchir au fait que si l'électronique était purement linéaire... nous ne nous amuserions pas avec les transistors, ... en fait vous ne seriez pas en train de lire ces lignes". - Fliess.
Références
Note aux lecteurs techniques : ce texte n'est pas précis. Vous trouverez un texte techniquement rigoureux, mais néanmoins compréhensible, dans ce magnifique livre du professeur Steven Strogatz.
1 La dynamique du cyclisme fait toujours l'objet de recherches actives, par exemple dans le cadre du développement de vélos qui favorisent la stabilisation. Voir la conférence TED du professeur Arend Schwab.
2 Beaucoup de choses ont été écrites sur la stabilité du système solaire. Un court texte se trouve dans cette lettre du professeur Scott Tremaine.
3 Le professeur Marten Scheffer a écrit un excellent livre sur cet exemple et bien d'autres.




