Understanding the shape of stability

Every morning, to get to EPFL, I channel my inner Mathieu van der Poel and pedal over the hills of Lausanne. Even with my clumsiness and before having a sufficient number of coffees, I don't fall, typically. Pebbles on the road, a gust of wind, or a quick turn to avoid crossing cows (we are in the Alps, after all) are all perturbations that can be easily handled, seemingly without any effort. This has little to do with my bike handling skills, and everything to do with the mathematical notion of stability.1
Simply put, a system – for instance, me on the bike – is said to be stable* when it always returns to its nominal state under small perturbations. This is exactly what we experience. A gust of wind does push me around a bit, but I always recover and return to my nominal state of going straight ahead.
You experience similar phenomena when flying (think of turbulence), sailing (with almost constant perturbations in the form of wind and waves), or while taking the metro from Lausanne Flon to Lausanne Gare, which is a serious test for our internal balance system.
So how might something fail to be stable? That happens when recovery from any arbitrarily small perturbation is not possible.
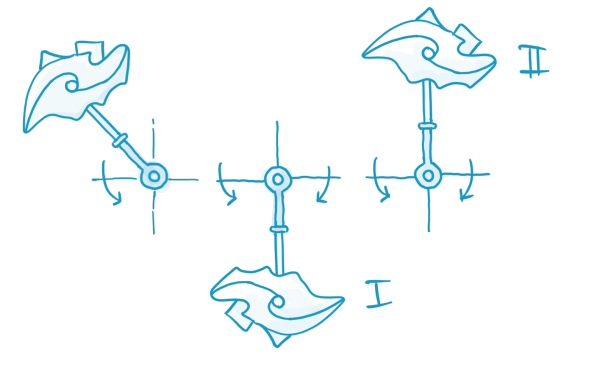
A telling example (which happens to be the cornerstone of a lot of analysis in our field) is the pendulum. Essentially a pendulum is a rod, mounted in such a way that it can freely rotate, with a sufficiently heavy end. In both State (I) and State (II) the pendulum is at rest, but note that only State (I) is stable: we can push the pendulum a bit and it will return to the rest state. If we push the pendulum in State (II), even very slightly, it will not return to State (II); State (II) is unstable.
You can test this yourself: try to balance a pen upright on your hand and hold your hand still. What if you push the pen a bit? Of course, the difficulty in trying to balance the pen on your hand in the first place already tells the story. If you try this with various objects, you will notice that the “speed of falling” changes; a large stick with a heavy top behaves very differently to a ballpoint. You might wonder: if this fall were extremely slow, so slow that we humans could not observe it with our eyes, could we even comment on its stability?
All these examples are somewhat tangible, but the notion of stability stretches far beyond the mechanical realm. Especially in these less tangible settings, we would like to understand stability by methods that are more comprehensive than simply what we see it. Think about the solar system: we don't know where we come from, but can we at least say where we are going? Ten billion years from now, will we still be moving around the sun?
This example is fascinating for a number of reasons. First of all, to talk about stability you must have some understanding of the behaviour of the system. What is normal, what is desired? The desire to improve our understanding here inspired entire branches of mathematics and physics. Second, the huge scale involved heavily complicates physical experiments, and to some extent measurements, so ideally, we would like to just analyse the mathematical models from physics to draw our conclusions. Attempting to answer these questions has driven an ongoing effort ever since the time of Newton.2
What if small changes become big changes?
Evidently, understanding the stability of the solar system is important, but we face more pressing issues: consider climate change. The climate, as a system, is highly complicated and the subject of extensive study. Let us focus on one particular example, the so-called ice-albedo system. Under ideal conditions, the amount of sunlight absorbed by our oceans and land is in balance with the amount of sunlight that is reflected by the ice on our polar caps. Better yet, under ideal conditions we might hope that this system is stable; that is, small variations in the amount of water, land and ice do not significantly alter temperature on earth. However, if the ice-albedo system is sufficiently perturbed, for instance by introducing excessive greenhouse gases, the melting polar caps break this balance. As a result, less sunlight is reflected, the earth heats up, more ice melts and so forth, forming a destructive feedback loop.3 This shows how a change in the system can alter stability, for instance from stable to unstable. Understanding this is critical, especially in the context of climate change.
Many more examples can be found, with a lot of research focusing on the life sciences. In medicine, for example, you might have an unstable system (think of cancer) that you want to render stable (stop the tumour growth and annihilate the cancer). In this case we want to stabilise the system. Differently put, we don’t want only to describe the dynamics of a system, we want to understand what can be prescribed; this is the study of control theory.
The examples we have seen so far are all physical, yet when you check the news, everything is “online” and “AI”. Is this new online reality stable? Well, this is the topic of active research, but let me provide you again with some examples. For instance, a streaming service like Spotify recommends music based on what you and your peers listen to. As a user, you want this to be stable; after listening to your favourite thrash metal bands for years, a single listen to the Barbie soundtrack shouldn’t drastically change your playlists. (Your neighbours might disagree.)
If you’ve read a previous NCCR blog post on gradient descent, that provides a more technical example. When applied to a convex problem, the process is stable; when applied to a non-convex problem, we might get stuck. That is, in the language from above, we do not always “recover” from being perturbed away from the optimizer. When it comes to algorithms, you might think of more aspects that can compromise stability: imperfect data (for example, blurry images used for object recognition), or simply the fact that digital machines work with finite precision (we cannot store infinitely long sequences of numbers on a computer).
By now, you probably agree that stability is important, yet not straightforward to identify, let alone impose. Moreover, we hope these examples have convinced you that 300 years after Newton it is still worthwhile studying stability; perhaps now more than ever.
What does shape have to do with it?
In studying stability, we focus in particular on understanding when stabilisation is possible. What features enable a system to achieve stability – or prohibit it?
Although it’s not the most exciting example, let's go back to the pendulum. We said that State (I) (hanging down) is stable, but we can be more precise. State (I) is stable with respect to any perturbation, except if we somehow end up in State (II) (being at rest in the upward position). Differently put, State (I) is an almost globally stable state of the pendulum system.
To understand this better, imagine the pendulum as being a ball rolling on the ridge of a hill, as illustrated in Figure 3. Again, the ball can be at rest in either State (I) or State (II). But State (I) is almost globally stable, while State (II) is again unstable. Can we smoothly deform the ridge in such a way that State (I) is globally stable? That would mean, along the entire ridge path, there should be only one position where the ball could come to rest.

To test this, take an empty toilet roll and a pair of scissors. Can you cut out a smooth curve that has either just a “valley” (like State (I) of the pendulum), or just a “mountain top” (like State (II))? Sadly, that doesn’t work: you can’t have the peak without the valley, and vice versa. So it is impossible, with any variation of this shape, to achieve global stability.
The crux here is the circular shape of our ridge. Any movement away from the peak means going downhill; but at some point, as you travel around the peak, you would start heading uphill (or else we would be in Escher's world)… and that creates a second point where our imaginary ball can be at rest. The shape of the circle obstructs global stability.
This simple observation is important as it allows us to draw fairly strong conclusions, based on few assumptions. We did not need to be bothered with how oddly shaped our pendulum is, only with the shape of its path. This is what interests me. Together with several colleagues, and with support from the Swiss National Science Foundation, I have been investigating how the underlying “shape” of a system dictates what is possible, going far beyond a point on a circle.
One of the main insights is that for truly non-linear problems, the underlying topology plays a key role – perhaps the key role – in understanding, and potentially achieving, stability.
And the world is non-linear…
“To appreciate what we are hinting at, it might be good to reflect that if electronics was purely linear... we would have no fun with transistors, ...in fact you would not be reading these lines.” — Fliess.
References
Note for technical readers: This text is not precise. For a technically rigorous, yet also accessible, text, see this wonderful book by Prof. Steven Strogatz.
1 The dynamics of cycling is still actively studied, for instance, in designing bicycles that aid in stabilisation. See the TED talk by Prof. Arend Schwab.
2 A lot has been written about stability of the solar system. For a short text, consider this letter by Prof. Scott Tremaine.
3 Prof. Marten Scheffer has written an outstanding book on this and many more examples.




