Die Form der Stabilität verstehen

Jeden Morgen, um zur EPFL zu gelangen, lasse ich meinen inneren Mathieu van der Poel walten und strample über die Hügel von Lausanne. Trotz meiner Ungeschicklichkeit und bevor ich genügend Kaffee getrunken habe, stürze ich normalerweise nicht. Kieselsteine auf der Straße, ein Windstoß oder ein schnelles Abbiegen, um Kühen auszuweichen (wir sind schließlich in den Alpen) sind alles Störungen, die sich scheinbar mühelos bewältigen lassen. Das hat wenig mit meinen Fähigkeiten im Umgang mit dem Fahrrad zu tun und alles mit dem mathematischen Begriff der Stabilität.1
Einfach ausgedrückt: Ein System - z. B. ich auf dem Fahrrad - gilt als stabil, wenn es bei kleinen Störungen immer wieder in seinen Sollzustand zurückkehrt. Das ist genau das, was wir erleben. Eine Windböe stößt mich zwar ein wenig herum, aber ich erhole mich immer wieder und kehre in meinen nominalen Zustand zurück, in dem ich geradeaus fahre. Ähnliche Phänomene werden erleben beim Fliegen (denke an Turbulenzen), beim Segeln (mit fast ständigen Störungen in Form von Wind und Wellen) oder bei der Fahrt mit der Metro von Lausanne Flon nach Lausanne Gare, die eine ernsthafte Prüfung für unser inneres Gleichgewichtssystem darstellt.
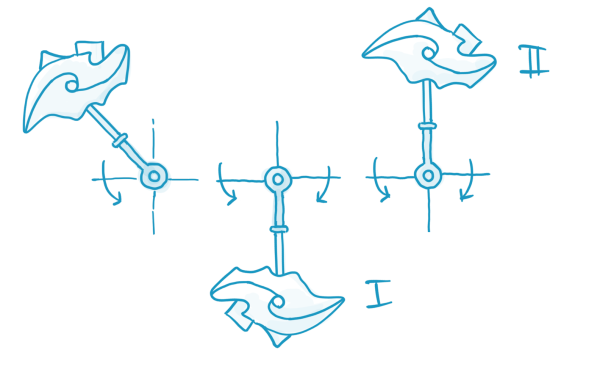
Wie kann also etwas nicht stabil sein? Das ist dann der Fall, wenn eine Erholung von einer beliebig kleinen Störung nicht möglich ist. Ein anschauliches Beispiel (das zufällig der Eckpfeiler vieler Analysen in unserem Bereich ist) ist das Pendel. Ein Pendel ist im Wesentlichen eine Stange, die so angebracht ist, dass sie sich frei drehen kann, mit einem ausreichend schweren Ende. Sowohl im Zustand (I) als auch im Zustand (II) befindet sich das Pendel in Ruhe, aber nur der Zustand (I) ist stabil: Wir können das Pendel ein wenig anstoßen und es kehrt in den Ruhezustand zurück. Wenn wir das Pendel im Zustand (II) schieben, und sei es nur ganz leicht, kehrt es nicht in den Zustand (II) zurück; der Zustand (II) ist instabil.
Dies könntest du selbst testen: Versuche, einen Stift aufrecht auf deiner Hand zu balancieren und deine Hand still zu halten. Was passiert, wenn der Stift ein wenig verschoben wird? Die Schwierigkeit, den Stift überhaupt auf der Hand zu balancieren, sagt natürlich schon alles. Versuchst du dies mit verschiedenen Gegenständen, wirst du feststellen, dass sich die "Fallgeschwindigkeit" ändert; ein großer Stock mit einer schweren Spitze verhält sich ganz anders als ein Kugelschreiber. Man könnte sich fragen: Wenn dieser Fall extrem langsam wäre, so langsam, dass wir Menschen ihn nicht mit unseren Augen beobachten könnten, könnten wir dann überhaupt etwas über seine Stabilität sagen?
Alle diese Beispiele sind einigermaßen greifbar, aber der Begriff der Stabilität reicht weit über den mechanischen Bereich hinaus. Vor allem in diesen weniger greifbaren Bereichen möchten wir die Stabilität mit Methoden verstehen, die umfassender sind als das, was wir einfach sehen. Denke an unser Sonnensystem: Wir wissen nicht, woher wir kommen, aber können wir wenigstens sagen, wohin wir gehen? Werden wir uns in zehn Milliarden Jahren immer noch um die Sonne bewegen?
Dieses Beispiel ist aus einer Reihe von Gründen faszinierend. Zunächst einmal muss man, um über Stabilität zu sprechen, das Verhalten des Systems verstehen. Was ist normal, was ist erwünscht? Das Bestreben, dieses Verständnis zu verbessern, hat ganze Zweige der Mathematik und Physik inspiriert. Zweitens werden physikalische Experimente und bis zu einem gewissen Grad auch Messungen durch die enormen Ausmaße, um die es hier geht, stark erschwert, so dass wir im Idealfall nur die mathematischen Modelle der Physik analysieren möchten, um unsere Schlussfolgerungen zu ziehen. Der Versuch, diese Fragen zu beantworten, ist seit Newton ein ständiges Bestreben.2
Was ist, wenn kleine Veränderungen zu grossen Veränderungen werden?
Natürlich ist es wichtig, die Stabilität des Sonnensystems zu verstehen, aber wir stehen vor dringenderen Fragen: Denke an den Klimawandel. Das Klima als System ist äußerst kompliziert und Gegenstand umfangreicher Studien. Konzentrieren wir uns auf ein besonderes Beispiel, das so genannte Eis-Albedo-System. Unter idealen Bedingungen steht die Menge des von unseren Ozeanen und dem Land absorbierten Sonnenlichts im Gleichgewicht mit der Menge des Sonnenlichts, die vom Eis unserer Polkappen reflektiert wird. Besser noch, unter idealen Bedingungen können wir hoffen, dass dieses System stabil ist, d. h. dass kleine Schwankungen in der Wasser-, Land- und Eismenge die Temperatur auf der Erde nicht wesentlich verändern.
Wird das Eis-Albedo-System jedoch in ausreichendem Masse gestört, beispielsweise durch die Zufuhr übermässiger Treibhausgase, wird dieses Gleichgewicht durch das Schmelzen der Polkappen gestört. Infolgedessen wird weniger Sonnenlicht reflektiert, die Erde erwärmt sich, mehr Eis schmilzt und so weiter, wodurch eine destruktive Rückkopplungsschleife entsteht.3
Dies zeigt, wie eine Veränderung des Systems die Stabilität verändern kann, zum Beispiel von stabil zu instabil. Dies zu verstehen, ist von entscheidender Bedeutung, insbesondere im Zusammenhang mit dem Klimawandel. Es gibt noch viele weitere Beispiele, wobei sich ein Großteil der Forschung auf die Biowissenschaften konzentriert. In der Medizin könnte man zum Beispiel ein instabiles System haben (man denke an Krebs), das man stabilisieren möchte (das Tumorwachstum stoppen und den Krebs vernichten). In diesem Fall wollen wir das System stabilisieren. Anders ausgedrückt: Wir wollen nicht nur die Dynamik eines Systems beschreiben, sondern auch verstehen, was man vorschreiben kann; das ist die Aufgabe der Kontrolltheorie.
Die Beispiele, die wir bisher gesehen haben, sind alle physikalisch, aber wenn man die Nachrichten verfolgt, ist alles "online" und "KI". Ist diese neue Online-Realität stabil? Nun, das ist das Thema aktiver Forschung, aber ich kann einige Beispiele anführen. Ein Streaming-Dienst wie Spotify empfiehlt dir Musik, die auf dem basiert, was du und deine Kollegen hören. Als Nutzer möchtest du, dass diese Empfehlungen stabil sind; nachdem du jahrelang Ihre Lieblings-Thrash-Metal-Bands gehört hast, sollte ein einziges Mal, wenn du den Barbie-Soundtrack hörst, deine Wiedergabelisten nicht drastisch verändern. (Deine Nachbarn sind da vielleicht anderer Meinung.)
Hast du einen früheren NCCR-Blogbeitrag über den Gradientenabstieg schon gelesen, finden Sie dort ein etwas technischeres Beispiel. Bei der Anwendung auf ein konvexes Problem ist der Prozess stabil; bei der Anwendung auf ein nicht-konvexes Problem könnten wir stecken bleiben. Das heisst, in der Sprache von oben, wir "erholen" uns nicht immer davon, dass wir vom Optimierer weggestört wurden. Bei Algorithmen fallst dir vielleicht noch weitere Aspekte ein, die die Stabilität beeinträchtigen können: unvollkommene Daten (z. B. unscharfe Bilder bei der Objekterkennung) oder einfach die Tatsache, dass digitale Maschinen mit endlicher Präzision arbeiten (wir können keine unendlich langen Zahlenfolgen auf einem Computer speichern).
Inzwischen stimmst du wahrscheinlich zu, dass Stabilität wichtig ist, aber nicht einfach zu erkennen, geschweige denn zu erzwingen. Wir hoffen, dass diese Beispiele dich davon überzeugt haben, dass es sich 300 Jahre nach Newton immer noch lohnt, sich mit Stabilität zu befassen, vielleicht sogar mehr denn je.
Was hat die Form damit zu tun?
Bei der Untersuchung der Stabilität konzentrieren wir uns vor allem darauf, zu verstehen, wann eine Stabilisierung möglich ist. Welche Eigenschaften ermöglichen es einem System, Stabilität zu erreichen - oder verhindern sie?
Obwohl es nicht das aufregendste Beispiel ist, kommen wir auf das Pendel zurück. Wir haben gesagt, dass der Zustand (I) (nach unten hängend) stabil ist, aber wir können noch präziser sein. Der Zustand (I) ist gegenüber jeder Störung stabil, es sei denn, wir gelangen irgendwie in den Zustand (II) (Ruhezustand in der Aufwärtsposition). Anders ausgedrückt: Zustand (I) ist ein nahezu global stabiler Zustand des Pendelsystems.
Um dies besser zu verstehen, kannst du dir das Pendel wie eine Kugel vorstellen, die auf dem Kamm eines Hügels rollt, wie in Abbildung 3 dargestellt. Auch hier kann die Kugel entweder im Zustand (I) oder im Zustand (II) ruhen. Der Zustand (I) ist jedoch fast global stabil, während der Zustand (II) wiederum instabil ist. Können wir den Grat so verformen, dass der Zustand (I) global stabil ist? Das würde bedeuten, dass es auf dem gesamten Weg des Grats nur eine einzige Stelle gibt, an der die Kugel zur Ruhe kommen kann.

Um dies zu testen, nimm eine leere Toilettenpapierrolle und eine Schere. Kannst du eine glatte Kurve ausschneiden, die entweder nur ein "Tal" (wie Zustand (I) des Pendels) oder nur eine "Bergspitze" (wie Zustand (II)) hat? Leider funktioniert das nicht: Man kann den Gipfel nicht ohne das Tal haben, und umgekehrt. Es ist also unmöglich, mit irgendeiner Variante dieser Form eine globale Stabilität zu erreichen.
Der Knackpunkt ist die Kreisform unseres Bergrückens. Jede Bewegung vom Gipfel weg bedeutet, dass es bergab geht; aber irgendwann, wenn man den Gipfel umrundet, geht es bergauf (sonst wären wir in Eschers Welt)... und das schafft einen zweiten Punkt, an dem unsere imaginäre Kugel in Ruhe sein kann. Die Form des Kreises behindert die globale Stabilität.
Diese einfache Beobachtung ist wichtig, denn sie erlaubt es uns, auf der Grundlage weniger Annahmen ziemlich eindeutige Schlussfolgerungen zu ziehen. Wir brauchten uns nicht damit zu befassen, wie seltsam unser Pendel geformt ist, sondern nur mit der Form seiner Bahn. Das ist es, was mich interessiert. Zusammen mit mehreren Kollegen und mit Unterstützung des Schweizerischen Nationalfonds habe ich untersucht, wie die zugrundeliegende "Form" eines Systems vorgibt, was möglich ist, weit über einen Punkt auf einem Kreis hinaus.
Eine der wichtigsten Erkenntnisse ist, dass bei wirklich nichtlinearen Problemen die zugrundeliegende Topologie eine Schlüsselrolle - vielleicht sogar die Schlüsselrolle - für das Verständnis und das mögliche Erreichen von Stabilität spielt.
Und die Welt ist nichtlinear...
"Um zu verstehen, worauf wir hinauswollen, ist es vielleicht gut, darüber nachzudenken, dass, wenn die Elektronik rein linear wäre... wir keinen Spass mit Transistoren hätten, ...dann würden Sie diese Zeilen nicht lesen." - Fliess.
Referenzen
Hinweis für technische Leser: Dieser Text ist nicht präzise. Einen technisch strengen, aber dennoch verständlichen Text ist in diesem wunderbaren Buch von Prof. Steven Strogatz zu finden.
1 Die Dynamik des Radfahrens wird immer noch aktiv erforscht, zum Beispiel bei der Entwicklung von Fahrrädern, die die Stabilisierung unterstützen. Siehe den TED-Vortrag von Prof. Arend Schwab.
2 Über die Stabilität des Sonnensystems ist viel geschrieben worden. Ein kurzer Text findet sich in diesem Brief von Prof. Scott Tremaine.
3 Prof. Marten Scheffer hat ein hervorragendes Buch über dieses und viele weitere Beispiele geschrieben.




