Comprendere la forma della stabilità

Ogni mattina, per raggiungere l'EPFL, mi incanalo nel Mathieu van der Poel che è in me e pedalo sulle colline di Losanna. Anche con la mia goffaggine e prima di aver bevuto un numero sufficiente di caffè, in genere non cado. I sassolini sulla strada, una folata di vento o una rapida sterzata per evitare di incrociare le mucche (siamo sulle Alpi, dopotutto) sono tutte perturbazioni che possono essere facilmente gestite, apparentemente senza alcuno sforzo. Questo ha poco a che fare con la mia abilità nel maneggiare la bicicletta e tutto a che fare con la nozione matematica di stabilità.1
In parole povere, un sistema - per esempio, io sulla bicicletta - si dice stabile* quando ritorna sempre al suo stato nominale sotto piccole perturbazioni. Questo è esattamente ciò che sperimentiamo. Una folata di vento mi spinge un po', ma mi riprendo sempre e torno al mio stato nominale di andare dritto.
Fenomeni simili si verificano quando si vola (si pensi alle turbolenze), quando si naviga (con perturbazioni quasi costanti sotto forma di vento e onde) o quando si prende la metropolitana da Losanna Flon a Losanna Gare, che è una prova seria per il nostro sistema di equilibrio interno.
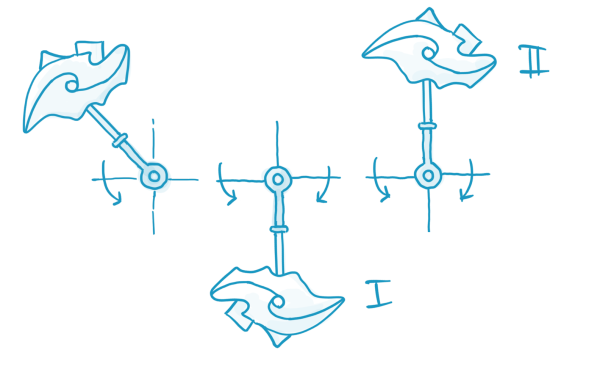
Come può qualcosa non essere stabile? Succede quando il recupero da una perturbazione arbitrariamente piccola non è possibile. Un esempio eloquente (che si dà il caso sia la chiave di volta di molte analisi nel nostro campo) è il pendolo. Essenzialmente un pendolo è un'asta, montata in modo da poter ruotare liberamente, con un'estremità sufficientemente pesante. Sia nello Stato (I) che nello Stato (II) il pendolo è a riposo, ma si noti che solo lo Stato (I) è stabile: possiamo spingere un po' il pendolo e tornerà allo stato di riposo. Se spingiamo il pendolo nello Stato (II), anche se di poco, non tornerà allo Stato (II); lo Stato (II) è instabile.
Potete verificarlo voi stessi: provate a tenere una penna in equilibrio sulla mano e a tenerla ferma. Cosa succede se si spinge un po' la penna? Naturalmente, la difficoltà nel cercare di tenere in equilibrio la penna sulla mano è già un dato di fatto. Se provate a farlo con vari oggetti, noterete che la "velocità di caduta" cambia; un grosso bastone con la parte superiore pesante si comporta in modo molto diverso da una penna a sfera. Ci si potrebbe chiedere: se questa caduta fosse estremamente lenta, così lenta che noi umani non potremmo osservarla con gli occhi, potremmo anche solo commentare la sua stabilità?
Tutti questi esempi sono in qualche modo tangibili, ma la nozione di stabilità va ben oltre l'ambito meccanico. Soprattutto in questi contesti meno tangibili, vorremmo capire la stabilità con metodi più completi rispetto alla semplice osservazione. Pensiamo al sistema solare: non sappiamo da dove veniamo, ma possiamo almeno dire dove stiamo andando? Tra dieci miliardi di anni, ci muoveremo ancora intorno al Sole?
Questo esempio è affascinante per una serie di motivi. Innanzitutto, per parlare di stabilità è necessario avere una certa comprensione del comportamento del sistema. Cosa è normale, cosa è desiderato? Il desiderio di migliorare la nostra comprensione ha ispirato intere branche della matematica e della fisica. In secondo luogo, l'enorme scala coinvolta complica pesantemente gli esperimenti fisici e, in una certa misura, le misurazioni; quindi, idealmente, vorremmo limitarci ad analizzare i modelli matematici della fisica per trarre le nostre conclusioni. Il tentativo di rispondere a queste domande ha guidato uno sforzo continuo fin dai tempi di Newton.2
Cosa succede se i piccoli cambiamenti diventano grandi cambiamenti?
È evidente che capire la stabilità del sistema solare è importante, ma ci troviamo di fronte a questioni più urgenti: pensiamo ai cambiamenti climatici. Il clima, come sistema, è molto complicato e oggetto di studi approfonditi. Concentriamoci su un esempio particolare, il cosiddetto sistema ghiaccio-albedo. In condizioni ideali, la quantità di luce solare assorbita dagli oceani e dalla terraferma è in equilibrio con la quantità di luce solare riflessa dai ghiacci delle calotte polari. Meglio ancora, in condizioni ideali potremmo sperare che questo sistema sia stabile; cioè, piccole variazioni nella quantità di acqua, terra e ghiaccio non alterano significativamente la temperatura sulla Terra.
Tuttavia, se il sistema ghiaccio-albedo viene sufficientemente perturbato, ad esempio con l'introduzione di un eccesso di gas serra, lo scioglimento delle calotte polari rompe questo equilibrio. Di conseguenza, la luce solare viene riflessa meno, la Terra si riscalda, si sciolgono altri ghiacci e così via, formando un ciclo di feedback distruttivo.3
Questo dimostra come un cambiamento nel sistema possa alterare la stabilità, ad esempio da stabile a instabile. Comprendere questo aspetto è fondamentale, soprattutto nel contesto del cambiamento climatico. Si possono trovare molti altri esempi, e molte ricerche si concentrano sulle scienze della vita. In medicina, ad esempio, si può avere un sistema instabile (si pensi al cancro) che si vuole rendere stabile (fermare la crescita del tumore e annientarlo). In questo caso vogliamo stabilizzare il sistema. In altre parole, non vogliamo solo descrivere la dinamica di un sistema, ma vogliamo capire cosa può essere prescritto; questo è lo studio della teoria del controllo.
Gli esempi che abbiamo visto finora sono tutti fisici, eppure quando si controllano le notizie, tutto è "online" e "AI". Questa nuova realtà online è stabile? Questo è un argomento di ricerca attiva, ma permettetemi di fornirvi ancora una volta alcuni esempi. Ad esempio, un servizio di streaming come Spotify consiglia musica in base a ciò che voi e i vostri coetanei ascoltate. Come utenti, volete che questo sia stabile; dopo aver ascoltato per anni le vostre band thrash metal preferite, un singolo ascolto della colonna sonora di Barbie non dovrebbe cambiare drasticamente le vostre playlist. (I vostri vicini potrebbero non essere d'accordo.)
Se avete letto un precedente post del blog NCCR sulla discesa del gradiente, questo fornisce un esempio più tecnico. Se applicato a un problema convesso, il processo è stabile; se applicato a un problema non convesso, potremmo bloccarci. In altre parole, nel linguaggio di cui sopra, non sempre ci "riprendiamo" da una perturbazione che ci allontana dall'ottimizzatore. Quando si parla di algoritmi, si potrebbe pensare ad altri aspetti che possono compromettere la stabilità: dati imperfetti (ad esempio, le immagini sfocate utilizzate per il riconoscimento degli oggetti), o semplicemente il fatto che le macchine digitali lavorano con precisione finita (non possiamo memorizzare sequenze di numeri infinitamente lunghe su un computer).
A questo punto, probabilmente sarete d'accordo sul fatto che la stabilità è importante, ma non è semplice da identificare, né tantomeno da imporre. Inoltre, speriamo che questi esempi vi abbiano convinto che 300 anni dopo Newton vale ancora la pena studiare la stabilità, forse ora più che mai.
Cosa c'entra la forma?
Nello studio della stabilità, ci concentriamo in particolare sul capire quando la stabilizzazione è possibile. Quali sono le caratteristiche che permettono a un sistema di raggiungere la stabilità o che la impediscono? Anche se non è l'esempio più entusiasmante, torniamo al pendolo. Abbiamo detto che lo stato (I) (sospeso verso il basso) è stabile, ma possiamo essere più precisi. Lo stato (I) è stabile rispetto a qualsiasi perturbazione, tranne nel caso in cui si finisca in qualche modo nello stato (II) (a riposo nella posizione verso l'alto). In altre parole, lo Stato (I) è uno stato quasi globalmente stabile del sistema pendolare.
Per capire meglio, immaginiamo il pendolo come una palla che rotola sul crinale di una collina, come illustrato nella Figura 3. Anche in questo caso, la palla può essere a riposo nella posizione di salita. Anche in questo caso, la palla può trovarsi a riposo nello Stato (I) o nello Stato (II). Ma lo Stato (I) è quasi globalmente stabile, mentre lo Stato (II) è nuovamente instabile. Possiamo deformare dolcemente la cresta in modo tale che lo Stato (I) sia globalmente stabile? Ciò significherebbe che, lungo l'intero percorso della cresta, dovrebbe esserci una sola posizione in cui la palla potrebbe fermarsi.

Per verificarlo, prendete un rotolo di carta igienica vuoto e un paio di forbici. Riuscite a ritagliare una curva liscia che abbia solo una "valle" (come lo stato (I) del pendolo) o solo una "cima" (come lo stato (II))? Purtroppo non funziona: non si può avere il picco senza la valle e viceversa. Quindi è impossibile, con qualsiasi variazione di questa forma, raggiungere la stabilità globale. Il punto cruciale è la forma circolare della nostra cresta. Qualsiasi movimento di allontanamento dal picco significa andare in discesa; ma a un certo punto, viaggiando intorno al picco, si inizierebbe a salire (altrimenti saremmo nel mondo di Escher)... e questo crea un secondo punto in cui la nostra palla immaginaria può essere a riposo. La forma del cerchio ostacola la stabilità globale.
Questa semplice osservazione è importante perché ci permette di trarre conclusioni abbastanza forti, basate su poche ipotesi. Non abbiamo bisogno di preoccuparci della forma strana del nostro pendolo, ma solo della forma del suo percorso. Questo è ciò che mi interessa. Insieme a diversi colleghi, e con il sostegno del Fondo Nazionale Svizzero per la Ricerca Scientifica, ho studiato come la "forma" sottostante di un sistema determini ciò che è possibile, andando ben oltre un punto su un cerchio.
Una delle principali intuizioni è che per i problemi veramente non lineari, la topologia sottostante gioca un ruolo chiave - forse il ruolo chiave - nella comprensione e nel potenziale raggiungimento della stabilità.
E il mondo è non lineare...
"Per apprezzare ciò a cui stiamo alludendo, potrebbe essere utile riflettere che se l'elettronica fosse puramente lineare... non ci divertiremmo con i transistor, ... infatti non stareste leggendo queste righe". - Fliess.
Riferimenti
Nota per i lettori tecnici: Questo testo non è preciso. Per un testo tecnicamente rigoroso, ma anche accessibile, si veda questo splendido libro del Prof. Steven Strogatz.
1 La dinamica del ciclismo è ancora attivamente studiata, ad esempio per la progettazione di biciclette che favoriscono la stabilizzazione. Si veda il discorso TED del Prof. Arend Schwab.
2 Molto è stato scritto sulla stabilità del sistema solare. Per un breve testo, si veda questa lettera del Prof. Scott Tremaine.
3 Il Prof. Marten Scheffer ha scritto un libro eccezionale su questo e molti altri esempi.




