How to teach a machine to drive

10-06-2022
Autonomous driving remains a major challenge in automation and control research. Members of the National Centre of Competence in Research (NCCR) Automation work on innovative approaches to solve aspects of this challenge.
car
Challenges still have to be overcome before cars can one day drive completely autonomously. Image: pxhere

You have to be familiar with traffic rules, be able to correctly assess challenging traffic situations in a split second and react accordingly. Anyone who has just had their first driving lesson can confirm that none of this is trivial. And so can those, who try to teach it to a machine.

Unlocking synergies

saber
Saber Salehkaleybar, co-author of this blog post, is a researcher at the EPFL. Image: EPFL

There are several approaches to this.

One of them is a machine learning technique called reinforcement learning (RL). Here, the correct decisions that a machine makes when driving a car - for example when it stops at a red light - are rewarded with the help of a so-called reward function. Researchers define what input features the machine should base its decisions on. This could be, for example, the location and speed of other cars, which the machine registers using camera images.

Another approach that has recently been successfully used to extract suitable input features in various complex tasks, such as playing video games or controlling robots, are so-called deep neural networks.

Combining the deep neural networks with the reinforcement learning technique therefore promises synergetic effects. Yet these synergies cannot fulfill their potential if the machine does not “understand” what the “proper behavior” is – i.e., the reward function is designed badly.

Devising a good reward function for autonomous driving remains challenging. Not least because it has proven enormously difficult to characterise the "proper" behaviour of human drivers.

So, instead of trying to define a “proper human driver behavior”, another way to unlock the synergies between reinforcement learning and deep neural networks is to let the machine extract that information itself.

Learning from Demonstration (LfD) is a paradigm for training machines to move in an environment based on demonstrations performed by a human driver. This can be done by directly mimicking the behavior of the human driver or by the autonomous design of a reward function from demonstrations. 

One of the main challenges in LfD is the possible mismatch between the human driver’s environment and that of the machine, which can and has caused the approach to fail in the past [1-4].

 

Pitfalls of incomplete information…

jalal
Jalal Etesami is co-writer of this blog post and a researcher at the EPFL. Image: EPFL

For example, researchers have used drones to record trajectories of humanly driven cars from a bird’s eye view and used these images as inputs to teach a machine how to drive. However, the drones had missed crucial elements in the environment that the human drivers had considered in their driving. For instance, the taillight of cars was not  always visible from drone images (as shown in Figure 1).

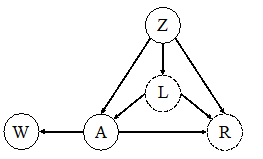
This environment can be abstracted by a so-called causal graph (see Figure 2), where the driver considers the velocity and location of front car (shown as covariate Z) and its taillight L in order to decide on the acceleration action A. In addition, the human driver’s action A influences the velocities and locations of cars in the rear, summarized as W.

The performance of the human driver is then evaluated with a latent reward signal R taking A, L, and Z as inputs. In this causal graph, the taillight L has a direct cause on both action A and reward Y but it is not observable by the machine. In fact, this taillight signal can be interpreted as a hidden confounder having direct influences on action and reward. This may lead to the machine inferring false effects of the human driver’s actions (such as W), which in turn can result in poor general performance in environments that differ from the one in which the machine observed the human driver’s actions [2].

figure 1 car
Figure 1. A driving scenario in the open source CARLA simulator  [5]: From left to right, the snapshots from inside the car, bird's eye view, and semantic segmentation - i.e., clustering parts of an image together which belong to the same object – are given for the ego car (the car at the center of bird’s eye view image). The taillight of the front car is not observable from the bird’s eye view. Thus, training a machine based on this view may result in poor general performance.

…and how we try to avoid them

To avoid such issues, we incorporate the underlying causal relationships in the environment into the training of the machine. In doing so, we aim to characterize theoretical limits of successful imitation in only partially observable systems. In particular, we would like to know which conditions are sufficient to guarantee that the performance of the machine is close to that of the human driver – especially when the machine is driving in new environments or lacks certain information.

Our approach is to first characterize the graphical criterion (for instance, whether there is no path between A and R that contains an arrow towards A) on the corresponding causal graph of the environment, under which imitation learning is feasible. Second, by exploiting the underlying causal graph, we will develop causal transfer learning approaches. This will make the Learning from Demonstration paradigm more robust against mismatches between the environments of machine and human driver.

figure 2 car
Figure 2. The corresponding causal graph of the environment in Figure 1: The human driver observes covariate Z and the taillight of front car to take action A. The reward signal R is a function of A, L, and Z. The variable W corresponds to the velocities and locations of cars in the back of ego car. The machine does not observe the variables shown by dashed circles.

The scientific method of Causal Imitation Learning

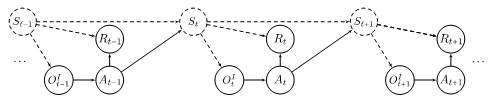
To formalize the imitation learning problem, we first introduce a set of notations. In our problem, the human driver performs her task in an environment that we call the source domain. At time t, the human driver is in state St. From this state, she observes OtE  (it is possible that OtE =St ) and accordingly selects an action At and gains reward Rt . She selects her action using a strategy  πE(At|OtE) that is a conditional probability distribution over all possible actions given the human driver’s observation.

 As an example, consider a driving scenario in which the human driver observes her location, other vehicles’ locations, her speed, her relative speed compared to her surrounding vehicles and the taillight of the care in front of her.

We denote all such variables by OtE . Suppose that the possible actions that the human driver can select from are either accelerate, decelerate, or keep her speed and turn left, turn right, or remain in her path.

In this example, πE(turn right, accelerate | OtE)=0.3  means that it is 30% likely that the human driver turns right and accelerates, given her observation OtE at time t .

 

figure 3 car
Figure 3. Causal graph of variables in the source domain. Dashed circles denote unobservable variables.   St, OtE, Ot, At, and Rt  represent the true state of the system, the human driver’s observation of that state, the machine’s observation of that state, the human driver’s action, and human driver’s reward all at time t , respectively.

As an observer, we partially observe the human driver’s behavior in the source domain over a period of length T . To be more precise, in our problem, we assume that at time 1≤t≤T, we observe a part of the human driver’s state, denoted by Ot , and her action At . For instance, in the driving example, if our observation from the human driver’s behavior is recorded by a drone, we can observe all variables in OtE  except the indicator light of the human driver’s front car, i.e., Ot=  {human driver’s location, other vehicles’ locations, human driver’s speed, relative speed of her surrounding vehicles}. In this case, OtE≠Ot . However, if our observation is recorded by a camera installed within the human driver’s vehicle, we have Ot=OtE . Figure 2 depicts the causal graph visualizing the relationships between the aforementioned variables, i.e., OtE, At, Ot, St,  and Rt  in the source domain.

Our observation from the human driver’s behavior is a trajectory of length T  which is given by O1,A1,…,OT,AT  and our goal is to design a strategy πI  so that the machine can mimic the human driver’s behavior, albeit, in a different environment. We call the separate environment the machine acts in, the target domain. In the target environment, similar to the source environment, at time t , the machine is in state St . From this state, it observes OtI  (it is possible that OtI=St ) and accordingly selects an action At  and gains reward Rt . Figure 3 depicts the causal graph of the variables in the target domain.

figure 4 car
Figure 4. Causal graph of variables in the target domain. Dashed circles denote unobservable variables.   St, OtI, At, and Rt  represent the true state of the system, machine’s observation from the state, machine’s action, and machine’s reward all at time t , respectively.

Strategies for different scenarios

Let us describe a particular setting, in which the machine can imitate the human driver perfectly. Assume the machine’s observation in the target domain is the same as the human driver's observation in the source domain. In other words, both the machine and the human driver have the same set of sensors for interacting with their environments, i.e., OtI=OtE. In this case, we can show that the optimal strategy for the machine is to estimate the human driver’s strategy in the source domain and apply it in the target environment. Although, the form of the optimal strategy is known but we may not be able to estimate it. This is because our observation from the source domain at time t  is limited to Ot,At  that may differ from the human driver's observation OtE,At  which we require to estimate her strategy. However, if the set of actions and states are finite, then using a set of linear equations, we can estimate the human driver’s strategy and consequently obtain the optimal strategy for the machine.

 

In general, imitating a human driver means that by applying our designed strategy (machine’s strategy), the machine behaves similar to the human driver. Given perfect observation, we can measure the difference between human driver and machine by a distance metric between two conditional distributions:

 

  1. the conditional probability of taking actions by the machine given the states in the target domain and
  2. the conditional probability of observing the same behavior by the human driver given the states in the source domain.

 

Our goal here is to select a strategy for the machine such that the mentioned distance is minimized, i.e., the machine drives almost identical to the human driver. Solving this problem in general is difficult. In our work, we aim to study the above imitation learning problem in different scenarios and either find the optimal strategy for the machine or propose a proxy strategy that has similar performance to the optimal strategy, i.e., the above distance for the proposed proxy strategy is bounded by a fixed amount.

 

 

Outlook

Overall, we aim to advance our understanding of limits of imitability in learning systems and study design of provably good LfDs with application to autonomous driving. Our approach incorporates causal models, which allow us to formulate mismatches between the human driver’s and the machine’s environments, characterize imitability, identify imitating strategy, and generalize beyond independent and identically distributed random settings.

 

 

References:

 

[1] J. Etesami and P. Geiger. “Causal transfer for imitation learning and decision making under sensor-shift.” In Proceedings of the 34th AAAI Conference on Artificial Intelligence, 2020.

[2] P. de Haan, D. Jayaraman, and S. Levine. “Causal confusion in imitation learning.” In Advances in Neural Information Processing Systems, 2019.

[3] J. Zhang, D. Kumor, and E. Bareinboim. “Causal Imitation Learning with Unobserved Confounders.” In Advances in neural information processing systems, 2020.

[4] F. Codevilla, E. Santana, A. M. López, and A. Gaidon. “Exploring the limitations of behavior cloning for autonomous driving.” In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019.

 

[5] A. Dosovitskiy, G. Ros, F. Codevilla, A. Lopez, and V. Koltun. “Carla: An open urban driving simulator.” In Conference on robot learning, 2017.